但从长远来看,许多事情也不会改变。一旦你掌握了这些底层技能,就刻意持续一生,这就是掌握了底层逻辑的好处。例如,算法。
当我们在前端谈论算法时,有两种观点:
有人认为算法在前端完全不重要,前端工程师没必要学算法。
也有人声称前端程序员也是程序员,需要深入学习算法,就像算法工程师一样。
我认为这两种观点都有些极端。
首先,算法在前端项目中也有很多应用。例如:
VirtualDOM 是 React 和 Vue 中的核心机制之一。它需要使用哈希表数据结构和diff算法。
在解析模板语法和生成 AST 时,我们需要使用树形数据结构。
浏览器的浏览历史,以及各种撤消和重做功能,都需要用到栈。
但同时我们也需要明白:前端更注重工程。
前端工程师最重要的是什么?在我看来,最重要的是工程能力。
所谓工程能力,本质上就是解决问题的能力。无论是编码技能还是架构思维,其本质都是服务于解决问题的最终目标。
完成项目是我们的终极目标,算法只是手段。
作为前端工程师,你不需要在算法领域投入太多精力。您无需获得 ACM 奖或完全理解厚书 Introduction to Algorithms。
所以在这里,我选择了前端面试中经常出现的算法题,然后经过总结整理,今天将其分享给你。
1、如何对数组进行排序?
排序算法是计算机科学中最古老、最基本的主题之一。大约有十几种常见的排序算法。
当然,我们不必完全掌握这些排序算法。如果我们需要先选择一个排序算法来学习,那么我认为应该是快速排序。
为什么?因为:
-
快速排序本身被广泛使用。
-
JavaScript 中 Array 的 sort 方法是通过 V8 引擎中的快速排序实现的。
(准确的说,当数组元素少于10个时,V8使用插入排序算法,当数组元素多于10个时,使用快速排序算法。)
“快速排序”的思路很简单,整个排序过程只需要三个步骤:
-
选择数组中的一个元素作为“枢轴”。我们可以选择任何元素作为枢轴,但中间的元素更直观。
-
所有小于枢轴的元素都被移动到枢轴的左侧;所有大于或等于枢轴的元素都被移动到枢轴的右侧。
-
对于枢轴左右的两个子集,重复第一步和第二步,直到所有子集中只剩下一个元素。
例如,我们有一个需要排序的数组:
let arr = [86, 24, 64, 48, 15, 30, 90, 49]
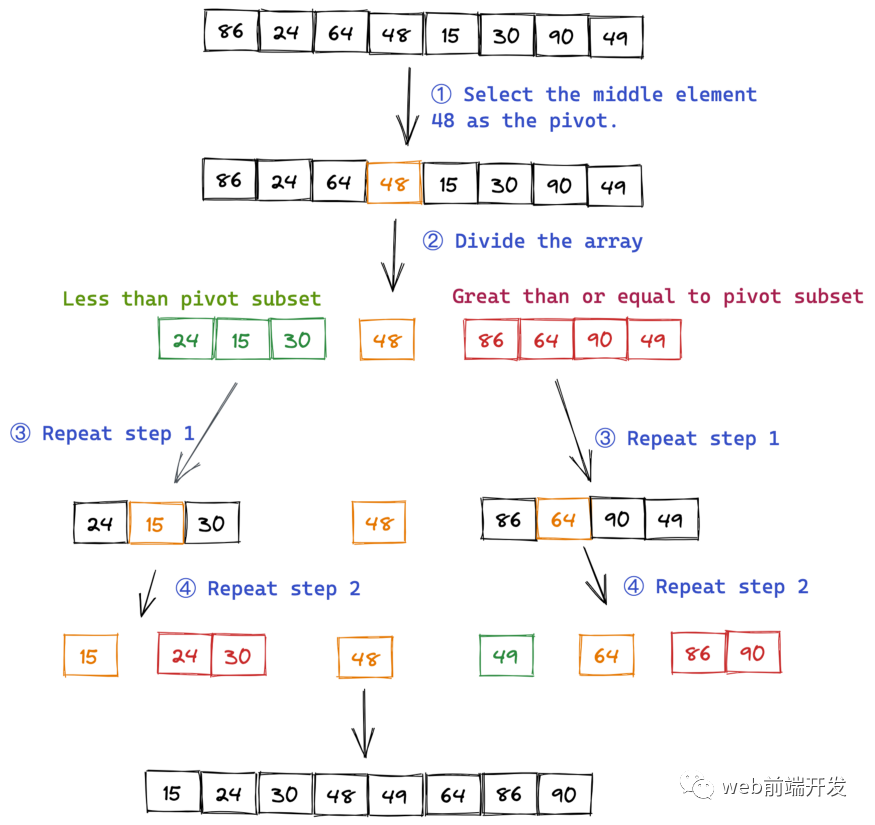
执行
首先,定义一个参数为数组的快速排序函数。
var quickSort = function(arr) {};
然后,检查数组中的元素个数,如果小于等于 1,则返回。
var quickSort = function(arr) { if (arr.length <= 1) { return arr; }};
接下来,选择枢轴,将其与原始数组分开,并定义两个空数组来存储两个子集。
var quickSort = function(arr) { if (arr.length <= 1) { return arr; } var pivotIndex = Math.floor(arr.length / 2) ; var pivot = arr.splice(pivotIndex, 1)[0]; var left = []; var right = []; };
然后,开始遍历数组,小于主元的元素放入左子集中,大于主元的元素放入右子集中。
var quickSort = function(arr) { if (arr.length <= 1) { return arr; } var pivotIndex = Math.floor(arr.length / 2) ; var pivot = arr.splice(pivotIndex, 1)[0]; var left = []; var right = []; for (var i = 0; i < arr.length; i++){ if (arr[i] < pivot) { left.push(arr[i]); } else { right.push(arr[i]); } } };
最后,通过使用递归重复这个过程,得到排序后的数组。
var quickSort = function(arr) { if (arr.length <= 1) { return arr; } var pivotIndex = Math.floor(arr.length / 2); var pivot = arr.splice(pivotIndex, 1)[0]; var left = []; var right = []; for (var i = 0; i < arr.length; i++){ if (arr[i] < pivot) { left.push(arr[i]); } else { right.push(arr[i]); } } return quickSort(left).concat([pivot], quickSort(right)); };
用法:

2、如何在排序后的数组中找到某个值?
对数组进行排序后,让我们使用排序后的数组。
假设我们有一个有序数组,我们想检查这个数组中是否存在某个值。那么我们应该怎么做呢?
我们可以遍历数组以确定该值是否存在于数组中,但是这种方法效率太低。
对于排序数组,我们有一个更有效的方法,就是二分查找。
执行二分搜索的基本步骤是:
-
以整个数组的中间元素作为搜索键开始。
-
如果搜索键的值等于项目,则返回搜索键的索引。
-
或者搜索键的值小于区间中间的项,则将区间缩小到下半部分。
-
否则,将其缩小到上半部分。
-
从第二点开始反复检查,直到找到值或区间为空。
例如,这是一个排序数组:
[15, 24, 30, 48, 49, 64, 86, 90, 100, 121, 130]
如果我们要检查这个数组中是否存在 48:
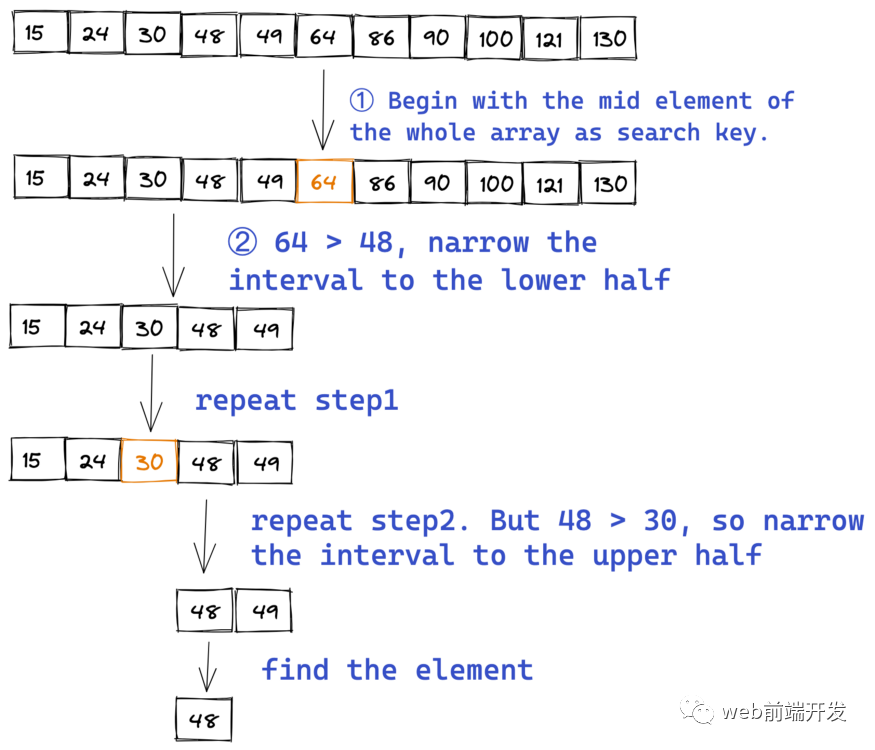
执行
function binarySearch(arr, x) { // left index of the current interval let l = 0; // right index of the current interval let r = arr.length - 1; // middle index of the current interval let mid; while (r >= l) { mid = l + Math.floor((r - l) / 2); // If the element is present at the middle // itself if (arr[mid] == x) { return mid; } // If element is smaller than mid, then // it can only be present in left subarray if (arr[mid] > x) { r = mid - 1; } // Else the element can only be present // in right subarray if (arr[mid] < x) { l = mid + 1; } } // We reach here when element is not // present in array return -1; }
用法:

比较
二分搜索比正常的线性搜索更快。
但是,你只能在排序数组上使用二进制搜索!
3、如何反转单链表?
链表是表示一系列节点的数据结构,其中每个节点包含两条信息:节点的值和指向列表中下一个节点的指针/引用。链表的开头称为头,链表末尾的节点称为尾,指向空值;null。
与数组相比,链表的主要好处是更容易在列表中插入或删除节点。另一方面,不允许随机访问数据,因为与数组不同,链表没有索引。
链表也广泛用于前端项目。例如,React 的 Fiber 使用链表。
我们可以这样创建一个链表:
function Node(value) { this.value = value this.next = null } let head = new Node(1) head.next = new Node(3) head.next.next = new Node(9) head.next.next.next = new Node(6) head.next.next.next.next = new Node(2)
如果我们被要求反转一个链表,我们需要让尾部成为头部:
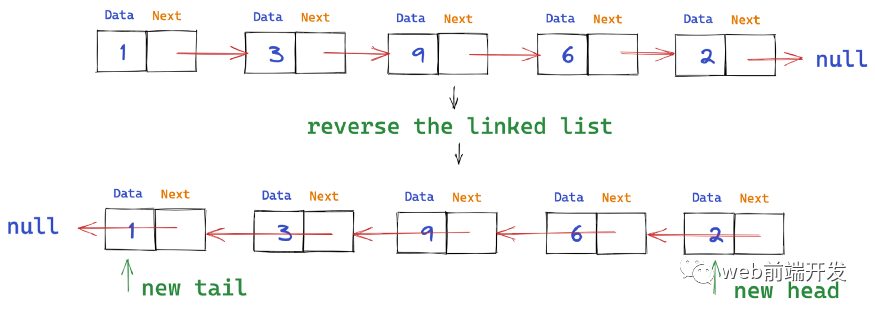
我们可以迭代或递归地反转链表,但我们将只关注通过以下步骤来解释今天的迭代方法:
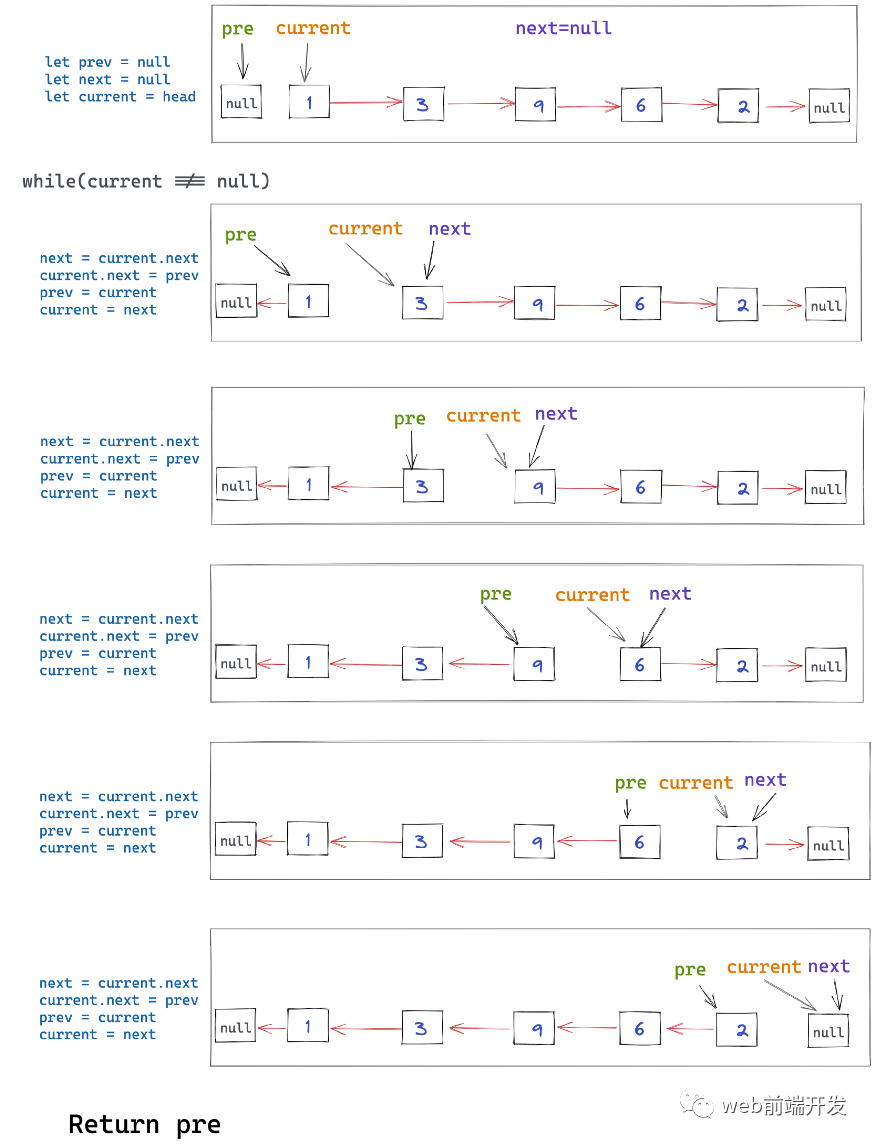
1)、初始化三个指针:prev、current 和 next:
-
prev:此指针将跟踪当前节点之前的节点,我们将其设置为空,因为单链表节点没有对其前一个节点的引用。
-
current:这个将从列表的头部开始,并跟踪我们当前所在的节点。
-
next:此指针将在其引用更改之前存储下一个节点,并且最初设置为 null。
2)、遍历所有节点,遍历链表,只要有节点,每次迭代执行以下操作:
-
设置为 current.next 的 next (我们需要在更改之前存储 current 的下一个节点)。
-
将 current.next 设置为 prev(我们现在可以通过反转链接来更改当前的下一个)。
-
将 prev 设置为 current(此步骤将前一个节点向前移动)。
-
设置当前等于下一个(这一步将当前节点向前移动)。
-
对所有节点重复步骤 2。
3)、 返回 prev 指针作为反向列表的新头。
const reverseList = head => { let prev = null let next = null let current = head while(current !== null){ next = current.next current.next = prev prev = current current = next } return prev }const reverseList = head => { let prev = null let next = null let current = head while(current !== null){ next = current.next current.next = prev prev = current current = next } return prev}
用图解释:
4、 如何检查括号是否有效?
前端开发经常需要解析模板语法,所以面试中经常会问到下面这个问题。
描述:
给定一个仅包含字符 ‘(‘, ‘)’, ‘{‘, ‘}’, ‘[‘ 和 ‘]’ 的字符串 s,确定输入字符串是否有效。
输入字符串在以下情况下有效:
-
括号必须用相同类型的括号闭合。
-
括号必须以正确的顺序闭合。
示例 1:
Input: s = "()"Output: true
示例2:
Input: s = "()[]{}"Output: true
示例3:
Input: s = "(]"Output: false
示例4:
Input: s = "([)]"Output: false
示例5:
Input: s = "{[]}"Output: true
约束:
-
1 <= s.length <= 104
-
s 仅包含括号 ‘()[]{}’。
分析:
对于这类问题,我们一般更喜欢使用栈数据结构。为什么可以用堆栈来完成?
想想有效的括号是什么意思?是对称的意思。
根据栈的后进先出原则,数据的入栈和出栈顺序是对称的。比如1、2、3、4、5、6依次入栈,对应的出栈顺序为6、5、4、3、2、1:
123456 654321
因此,你可以在这里记住一个规则:如果问题涉及括号或其他对称结构,则相关解决方案很可能与堆栈有关。
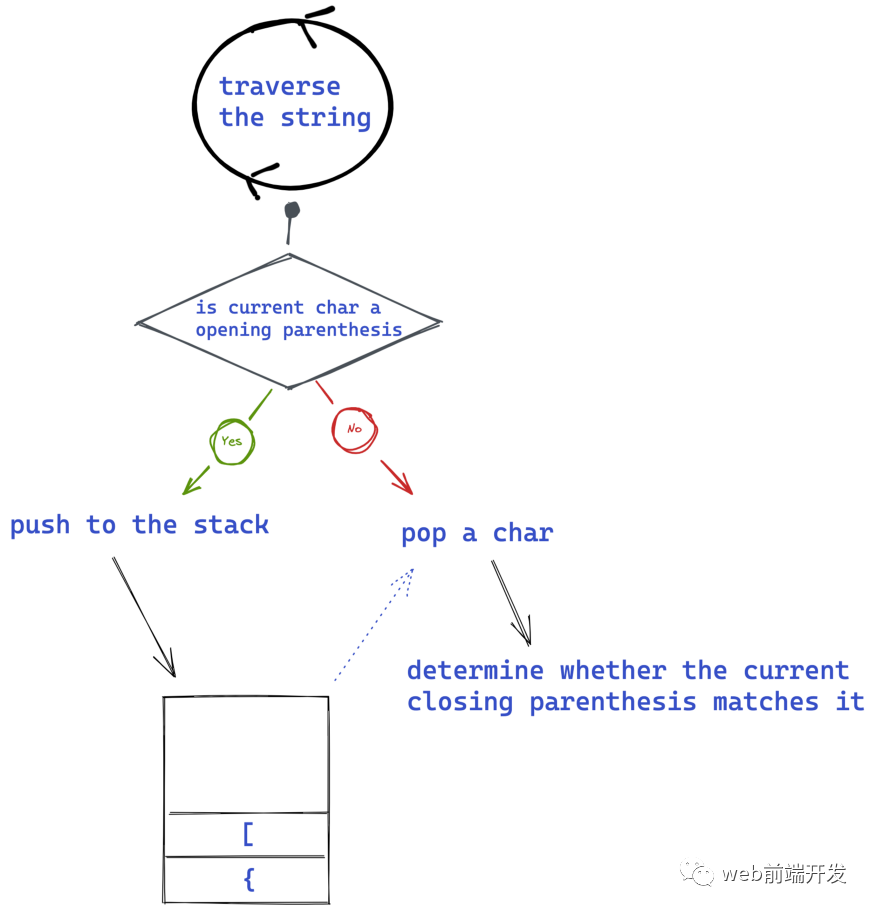
我们的想法是:遍历整个字符串:
-
如果找到左括号,则将其添加到堆栈中。
-
如果找到右括号,则弹出堆栈顶部的一个元素,并确定当前的右括号是否匹配它。
对于有效的括号,整个流程可能如下所示:
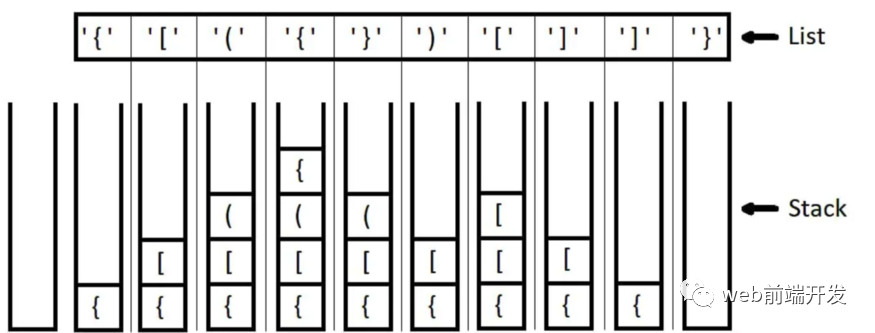
执行:
const isValid = function(s) { if (!s) { return true; } // array can be used as a stack const stack = []; const len = s.length; for (let i = 0; i < len; i++) { // cache const ch = s[i]; if (ch === "(" || ch === "{" || ch === "[") { stack.push(leftToRight[ch]); } else { // If the stack is not empty and the // openning parenthesis at the top of the stack does not // match the current character, it is invalid. if (!stack.length || stack.pop() !== ch) { return false; } } } // If all parentheses can be matched successfully, // then the final stack should be empty return !stack.length; };
总结
以上就是我分享的4个常见的算法问题。当然,这些内容还远远不够,但是由于文章篇幅关系,这次就不继续了。
很多初级前端开发者,尤其是自学成才的(比如我),面对面试可能会有点害怕,尤其是在我们不擅长的算法领域。
在面试前多练习算法题,为自己搭建知识库。提前准备有助于增强自信心。
面试的时候,积极思考自己的知识库和面试题之间的关系,然后多说自己擅长什么,即使内容和题本身关系不大。
面试结束后,主动与面试官沟通,问他问题的逻辑。同时,你可以把面试中不懂的问题记录下来,然后仔细研究。毕竟,这不会是你的最后一次面试。







留言
您必须登陆 才能发表评论。